TL;DR:
- Reservoir computing, a powerful machine learning tool, excels at modeling complex dynamic systems.
- Recent research touts its ability to predict chaotic system trajectories with minimal data.
- However, a new study reveals overlooked limitations in reservoir computing.
- Next-generation reservoir computing (NGRC) also faces challenges, particularly when vital system information is lacking.
- Traditional reservoir computing requires a lengthy “warm-up” period for accurate predictions.
- Addressing these limitations could enhance the utility of reservoir computing in dynamic system modeling.
Main AI News:
In the intricate realm of nonlinear dynamic systems, a ripple in one corner can unleash a tidal wave of changes elsewhere. Whether we peer into the complexities of our climate, delve into the mysteries of the human brain, or scrutinize the intricate dance of electrons on the electric grid, these systems undergo profound transformations over time. Due to their inherent capriciousness, modeling such dynamic systems has been a formidable challenge.
However, in the past two decades, a breakthrough has emerged in the form of reservoir computing—a deceptively simple yet remarkably potent machine-learning approach that has heralded success in modeling high-dimensional chaotic behaviors.
“Machine learning is increasingly being leveraged to decipher the enigma of dynamic systems for which we lack a robust mathematical description,” remarks Yuanzhao Zhang, an SFI Complexity Postdoctoral Fellow.
Recent research has celebrated the prowess of reservoir computing in predicting the trajectories of chaotic systems, even when equipped with minimal training data. Astonishingly, it can discern the ultimate destination of a system solely based on its initial conditions. Zhang, though intrigued, couldn’t help but maintain a degree of skepticism.
“The reports left me pondering—can this be the whole truth?” questions Zhang.
The answer he unearthed is nuanced. In a recent publication in Physical Review Research, Zhang and his collaborator, physicist Sean Cornelius from Toronto Metropolitan University, have exposed limitations in reservoir computing that have eluded the research community’s scrutiny thus far. They have illuminated a kind of Catch-22, which proves to be an intricate challenge to circumvent, particularly when dealing with complex dynamic systems.
“It’s one of those limitations that I believe hasn’t received the attention it deserves within the community,” Zhang asserts.
Reservoir computing, first conceptualized by computer scientists over two decades ago, stands as an agile predictive model constructed upon neural networks. It boasts simplicity and cost-effectiveness in training compared to other neural network frameworks.
In 2021, a groundbreaking evolution, known as next-generation reservoir computing (NGRC), emerged, offering several advantages over its conventional counterpart. Notably, NGRC demands less data for training. Recent explorations into its applications within machine learning have unveiled the potential of both RC and NGRC models in modeling dynamic systems with minimal data.
However, Zhang and Cornelius scrutinized both standard RC and NGRC, revealing their vulnerabilities in specific scenarios. “They both grapple with a Catch-22 dilemma, albeit of different natures.”
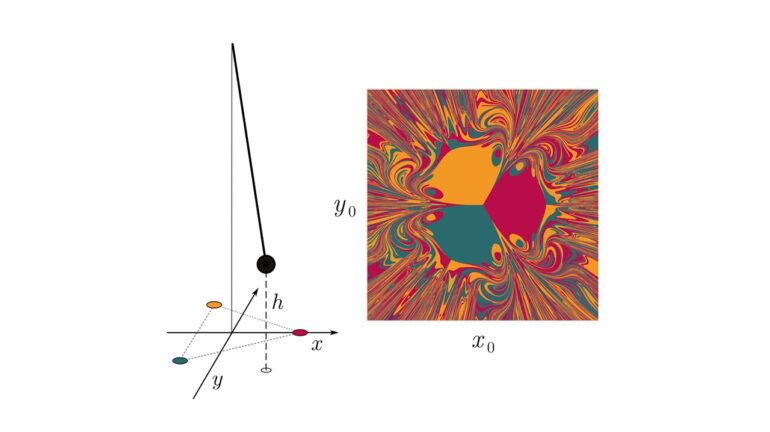
In their examination of NGRC, they observed a straightforward yet dynamic chaotic system—a pendulum with a magnet affixed to its end, swinging amid three fixed magnets forming a triangle on a level surface. When the system was provided with information about the required nonlinearity to describe itself, it excelled.
“In essence, the system receives a sneak peek of essential information prior to the commencement of training,” Zhang explains. However, if they perturbed the model? “It invariably yielded inaccurate predictions,” Zhang laments. This implies that the model’s predictive prowess relies heavily on the preexistence of crucial information about the system in question. As for RC, the researchers noted that it necessitated an extensive “warm-up” period, nearly as time-consuming as the dynamic movements of the magnet itself, to make accurate predictions.
Addressing these limitations in both RC and NGRC could potentially unlock the full potential of this burgeoning computing framework for researchers venturing into the realm of dynamic systems.
Conclusion:
The discovery of limitations in reservoir computing, both in its traditional form and as NGRC, highlights the need for caution when applying these techniques to complex dynamic systems. Researchers and businesses in the machine learning market should consider these constraints when exploring reservoir computing’s potential, especially in scenarios where comprehensive system information is lacking or a rapid response is required. Finding ways to mitigate these challenges will be crucial to harnessing the full power of reservoir computing in dynamic system modeling applications.