TL;DR:
- Researchers from Stanford and UT Austin introduced Contrastive Preference Learning (CPL).
- CPL offers a regret-based model of preferences for Reinforcement Learning from Human Feedback (RLHF).
- It eliminates the need for RL in the RLHF process, addressing high-dimensional state and action spaces.
- CPL combines the regret-based preference framework with the Maximum Entropy (MaxEnt) principle.
- Key benefits include scalability, off-policy operation, and applicability to diverse Markov Decision Processes (MDPs).
- CPL achieves efficient learning in sequential tasks, outperforming RL baselines in parameter efficiency and speed.
- It unlocks the potential to bypass RL and learn optimal policies directly from preferences.
Main AI News:
In the realm of AI, bridging the gap between human preferences and advanced pretrained models has emerged as a pivotal challenge. With the continuous improvement in model performance, ensuring alignment with human values becomes increasingly complex, especially when dealing with extensive datasets that inherently contain undesirable behaviors. In response to this challenge, Reinforcement Learning from Human Feedback (RLHF) has risen to prominence as a transformative approach.
RLHF leverages human preferences to discern acceptable from undesirable behaviors, ultimately refining established policies. This methodology has exhibited promising results in various applications, including the adaptation of robotic protocols, enhancement of image generation models, and the fine-tuning of large language models (LLMs), even when dealing with suboptimal data. The majority of RLHF algorithms follow a two-stage process.
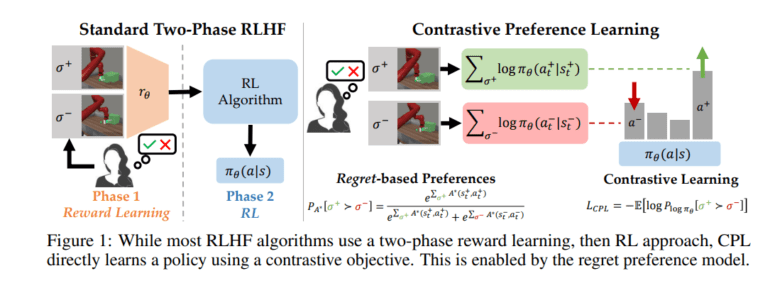
Initially, user preference data is collected to train a reward model, which is subsequently optimized by a standard reinforcement learning (RL) algorithm. However, recent research challenges the foundational assumptions of this two-phase paradigm. It suggests that human preferences should be rooted in the regret associated with each action under the expert’s reward function, rather than simply considering total rewards or partial returns.
Consequently, the optimal advantage function, also known as the negated regret, emerges as a more suitable metric for learning from feedback than traditional reward functions. This insight leads to the use of RL in the second phase of two-phase RLHF algorithms, introducing complexities related to temporal credit assignment and policy gradient instability. In practice, earlier works often resort to constrained assumptions to mitigate these challenges, such as adopting a contextual bandit formulation.
However, these assumptions do not fully capture the complexities of real-world scenarios, particularly in multi-step, sequential interactions. As a result, RLHF approaches inadvertently underestimate the role of human preferences in shaping policies.
In a groundbreaking departure from the conventional partial return model that relies on total rewards, a team of researchers from Stanford University, UMass Amherst, and UT Austin has introduced a novel family of RLHF algorithms. Their approach centers on a regret-based model of preferences, offering precise guidance on optimal actions. Notably, this innovation eliminates the need for RL, enabling the resolution of RLHF challenges within the context of high-dimensional state and action spaces, as defined by the Markov Decision Process (MDP) framework.
The researchers’ key breakthrough lies in establishing a direct link between advantage functions and policies by combining the regret-based preference framework with the Maximum Entropy (MaxEnt) principle. This approach leads to the development of Contrastive Preference Learning (CPL), a method that brings three substantial advantages over previous efforts.
First, CPL excels by matching optimal advantages solely through supervised learning objectives, obviating the need for dynamic programming or policy gradients. Second, CPL operates in a fully off-policy manner, making it adaptable to various offline data sources, even when they are less than ideal. Lastly, CPL empowers preference searches over sequential data, enabling learning across diverse Markov Decision Processes (MDPs).
Remarkably, CPL stands out as the first method to fulfill all three of these requirements simultaneously in the realm of RLHF techniques. The researchers showcase CPL’s capabilities in sequential decision-making tasks, utilizing suboptimal, high-dimensional off-policy data to demonstrate its alignment with the three tenets mentioned earlier. Notably, CPL proves its mettle by efficiently learning temporally extended manipulation rules in the MetaWorld Benchmark, employing the same fine-tuning process as dialogue models.
In precise terms, the researchers employ supervised learning from high-dimensional image observations to pre-train policies, subsequently fine-tuning them using preferences. CPL achieves performance on par with previous RL-based techniques, all without the complexities of dynamic programming or policy gradients. Additionally, CPL offers a remarkable fourfold improvement in parameter efficiency and a 1.6x increase in speed when compared to conventional RL baselines, especially when utilizing denser preference data. This innovative approach paves the way for a future where Reinforcement Learning (RL) can be bypassed through the application of Maximum Entropy, giving rise to Contrastive Preference Learning (CPL), a revolutionary algorithm that unlocks optimal policies from preferences without the need to learn reward functions.
Conclusion:
The introduction of Contrastive Preference Learning (CPL) marks a significant advancement in the field of Reinforcement Learning from Human Feedback (RLHF). CPL’s regret-based model of preferences and its ability to eliminate the need for RL brings scalability and flexibility to RLHF, making it adaptable to various real-world scenarios. This innovation not only enhances the efficiency of learning but also offers promising opportunities to streamline RL processes and improve the market’s adoption of RLHF in industries that rely on complex decision-making models.