TL;DR:
- AI and Deep Learning are driving technological advancements.
- They enable machines to learn from data and make decisions.
- Symbolic Regression plays a vital role in scientific research.
- Φ-SO, a Physical Symbolic Optimization framework, automates finding analytical expressions for complex datasets.
- Physics imposes strict unit limitations, challenging generic regression algorithms.
- Φ-SO utilizes deep reinforcement learning to respect unit constraints.
- It enhances model accuracy and interpretability through dimensional analysis.
- Φ-SO offers practical applications, even with noisy data.
- Tests show Φ-SO’s exceptional performance in physics equations.
- Φ-SO is a reliable tool for interpreting and forecasting cosmic occurrences.
Main AI News:
In the realm of cutting-edge technology, Artificial Intelligence (AI) and Deep Learning stand as monumental pillars, ushering in a new era of innovation and problem-solving. These transformative technologies have empowered robots to transcend the boundaries of human intelligence, undertaking tasks previously considered beyond their reach. AI’s profound impact resonates across diverse industries, driving revolutionary advancements and solutions. At its core, AI harnesses the power of vast data repositories to teach machines the art of decision-making and prediction. This pivotal role in scientific pursuits has birthed remarkable tools that have garnered immense acclaim within the AI community.
Within the realm of Artificial Intelligence, Symbolic Regression emerges as a key player in the intricate landscape of scientific exploration. Symbolic Regression revolves around algorithms designed to decode complex patterns and correlations concealed within datasets, automating the quest for analytical expressions. Scientists and researchers alike have invested considerable effort in unlocking the latent potential of Symbolic Regression.
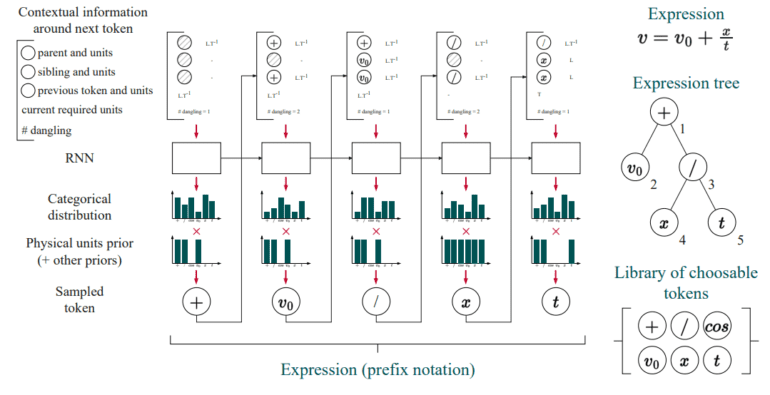
Delving deeper into the heart of Symbolic Regression, a dedicated team of researchers introduces Φ-SO, a groundbreaking Physical Symbolic Optimization framework. This innovative methodology confronts the intricacies of physics, where adherence to precise units is paramount. Φ-SO revolutionizes the process of uncovering analytical expressions that seamlessly fit complex datasets.
Physics presents a unique challenge due to its inherent demand for uniformity and precision. Generic symbolic regression algorithms often falter when confronted with the stringent unit constraints that underpin the world of physics. In stark contrast, Φ-SO emerges as a tailored solution to this predicament. Leveraging deep reinforcement learning techniques, it skillfully retrieves analytical symbolic expressions while ensuring strict adherence to the fundamental unit limitations imposed by physics.
Φ-SO has been meticulously crafted to craft solutions that seamlessly align with the uniformity of physical units. Furthermore, it enhances the accuracy and interpretability of resulting models by discerning improbable solutions and employing the structured principles of dimensional analysis. Beyond its theoretical implications, Φ-SO finds practical applications, extending its utility beyond noiseless data fitting. In the face of noisy data, it continues to provide invaluable analytical approximations, showcasing its adaptability and real-world practicality.
The team’s rigorous evaluation of Φ-SO involved subjecting it to a battery of tests on a standard benchmark comprising equations drawn from physics textbooks and the renowned Feynman Lectures on Physics. The results underscored Φ-SO’s exceptional performance, even when confronted with noise levels exceeding 0.1%. As a result, Φ-SO emerges as a dependable and precise instrument for deciphering and forecasting the dynamics of cosmic phenomena. In the ever-evolving landscape of AI and scientific exploration, Φ-SO shines as a beacon of promise and innovation.
Conclusion:
The introduction of Φ-SO marks a significant milestone in the field of Physical Symbolic Optimization. Its ability to navigate the complexities of physics and provide accurate analytical solutions, even in the presence of noise, positions it as a valuable tool for various industries. This innovation has the potential to streamline research, improve model accuracy, and enhance decision-making processes, making it a promising asset in the market for AI-driven solutions.