TL;DR:
- Researchers at MIT and IBM have developed physics-enhanced deep surrogate (PEDS) models.
- PEDS models use neural networks trained with physics simulators to solve complex equations.
- These models are up to three times more accurate than conventional neural networks.
- They require only 1,000 training points, reducing data needs significantly.
- Potential applications include accelerating simulations in engineering, weather forecasting, carbon capture, and nuclear reactors.
Main AI News:
In the realm of science and engineering, the enduring principles established by luminaries like Isaac Newton have provided the bedrock for understanding the natural world. These principles, encompassing optics, acoustics, engineering, and electronics, are underpinned by a foundational set of equations. Today, a groundbreaking development in the realm of artificial intelligence leverages brain-inspired neural networks to revolutionize the efficiency with which these equations are solved, offering immense potential for diverse applications in science and engineering.
Contemporary scientific and engineering endeavors often involve grappling with intricate partial differential equations. These equations serve as indispensable tools for modeling complex physical systems marked by multifaceted rates of change, spanning both spatial and temporal dimensions. Their utility extends to diverse domains, encompassing scenarios such as the aerodynamic characteristics of aircraft wings, the dispersion of pollutants in the atmosphere, and even the gravitational collapse of stars culminating in the formation of black holes.
Traditionally, scientists have relied on high-precision numerical methods to tackle the formidable challenges posed by these equations. While effective, these methods are frequently characterized by their time-consuming nature and voracious appetite for computational resources.
At present, an alternative approach in the form of data-driven surrogate models has gained traction. These models, prominently featuring neural networks, are trained using data derived from numerical solvers, enabling them to predict potential outcomes. However, a significant drawback lies in the substantial volume of training data required, a volume that escalates exponentially as these models expand in complexity. This inherent limitation hinders scalability, as observed by study lead author Raphaël Pestourie, a computational scientist at the Georgia Institute of Technology in Atlanta.
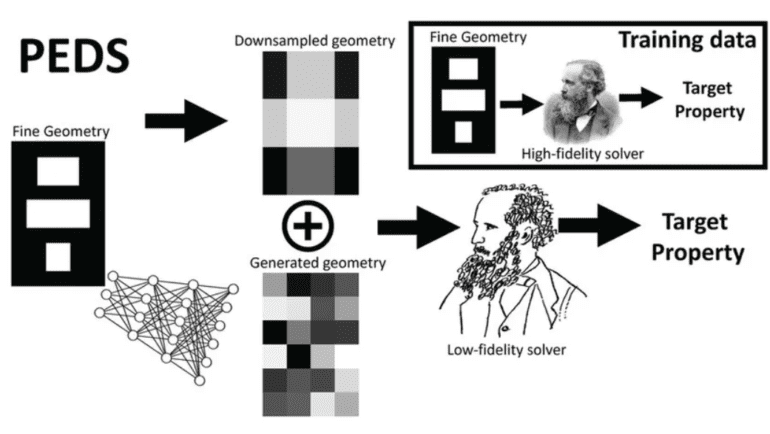
In a recent research undertaking, a novel methodology for developing surrogate models has emerged. This innovative approach harnesses the power of physics simulators to facilitate the training of neural networks, enabling them to mirror the precision achieved by high-precision numerical systems. The underlying objective is to obtain precise solutions by integrating domain expertise, in this case, physics principles, instead of resorting solely to brute-force computational methods.
This pioneering study introduced what the researchers coined as physics-enhanced deep surrogate (PEDS) models, subjecting them to rigorous testing across three distinct categories of physical systems: diffusion processes, exemplified by the spread of dye in a liquid over time; reaction-diffusion phenomena, manifesting in scenarios following chemical reactions; and electromagnetic scattering.
The results yielded a remarkable revelation – these novel models demonstrated an accuracy level up to three times superior to conventional neural networks in addressing partial differential equations. Intriguingly, the PEDS models necessitated a mere 1,000 training points, marking a substantial reduction in the requisite training data by a factor of at least 100 to achieve a target error rate of 5 percent.
Raphaël Pestourie elucidates the essence of this breakthrough: “The idea is quite intuitive—let the neural networks do the learning and the scientific model do the science. PEDS shows that combining both is far greater than the sum of its parts.”
Conclusion:
The implications of PEDS models are far-reaching, with the potential to expedite simulations for intricate systems ubiquitous in engineering, encompassing fields such as weather forecasting, carbon capture, and nuclear reactor modeling. As Pestourie aptly summarizes, these innovative models hold the promise of revolutionizing diverse domains and driving progress in the pursuit of scientific and engineering excellence.