- Cutting-edge deep neural networks (DNNs) benefit greatly from first-order optimizers but face challenges with large-scale model training.
- Second-order optimizers promise superior convergence but suffer from high computational and memory costs.
- A groundbreaking study introduces 4-bit Shampoo, a memory-efficient second-order optimizer, maintaining performance comparable to its 32-bit counterpart.
- The innovation lies in quantizing the eigenvector matrix of the preconditioner, preserving critical singular values crucial for accurate computation.
- Techniques such as Björck orthonormalization and linear square quantization enhance performance without sacrificing efficiency.
Main AI News:
Cutting-edge deep neural networks (DNNs) have revolutionized multiple domains, from computer vision to natural language processing, owing to their extraordinary performance. The efficacy of first-order optimizers such as stochastic gradient descent with momentum (SGDM) and AdamW has been instrumental in this success. However, the training of large-scale models with these methods often encounters efficiency challenges. Second-order optimizers like K-FAC, Shampoo, AdaBK, and Sophia offer superior convergence properties but are plagued by substantial computational and memory overheads, limiting their widespread adoption within constrained memory environments.
Efforts to alleviate memory consumption of optimizer states have predominantly focused on factorization and quantization techniques. Factorization employs low-rank approximations to represent optimizer states, a strategy utilized across both first and second-order optimizers. Conversely, quantization methods leverage low-bit representations to compress the conventional 32-bit optimizer states. While quantization has proven effective for first-order optimizers, extending its benefits to second-order optimizers presents unique hurdles due to the intricate matrix operations involved.
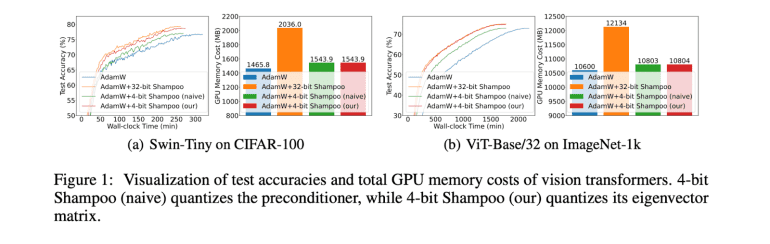
A groundbreaking study by researchers from Beijing Normal University and Singapore Management University introduces the first-ever 4-bit second-order optimizer, using Shampoo as a case study, while maintaining performance levels akin to its 32-bit counterpart. The innovation lies in quantizing the eigenvector matrix of the preconditioner within 4-bit Shampoo, rather than directly quantizing the preconditioner itself. This nuanced approach preserves the critical small singular values of the preconditioner, vital for accurate computation of the inverse fourth root, thereby averting performance degradation. Moreover, the computation of the inverse fourth root from the quantized eigenvector matrix remains straightforward, ensuring no increase in wall-clock time. The study proposes two techniques for performance enhancement: Björck orthonormalization to rectify the orthogonality of the quantized eigenvector matrix and linear square quantization, surpassing dynamic tree quantization for second-order optimizer states.
The crux of the methodology revolves around quantizing the eigenvector matrix U of the preconditioner A=UΛUT using a specialized quantizer Q, as opposed to directly quantizing A. This approach preserves the singular value matrix Λ, pivotal for precise computation of the matrix power A^(-1/4) through matrix decompositions like SVD. Björck orthonormalization corrects the loss of orthogonality in the quantized eigenvectors, while linear square quantization replaces dynamic tree quantization for superior 4-bit quantization performance. The preconditioner update leverages the quantized eigenvectors V and unquantized singular values Λ to approximate A≈VΛVT. The approximation of the inverse 4th root A^(-1/4) entails quantizing it to obtain its quantized eigenvectors and reconstructing it using the quantized eigenvectors and diagonal entries. Further orthogonalization facilitates accurate computation of matrix powers As for arbitrary s.
Extensive experimentation showcases the superiority of the proposed 4-bit Shampoo over first-order optimizers like AdamW. Despite necessitating 1.2x to 1.5x more epochs, leading to extended wall-clock times, first-order methods consistently achieve lower test accuracies compared to second-order optimizers. Conversely, 4-bit Shampoo achieves test accuracies comparable to its 32-bit counterpart, with differences ranging from -0.7% to 0.5%. The upticks in wall-clock time for 4-bit Shampoo span from -0.2% to 9.5% compared to 32-bit Shampoo, while delivering memory savings of 4.5% to 41%. Notably, the memory costs of 4-bit Shampoo merely surpass those of first-order optimizers by 0.8% to 12.7%, marking a substantial stride in facilitating the adoption of second-order methods.
This research underscores the significance of 4-bit Shampoo in enabling memory-efficient DNN training. By quantizing the eigenvector matrix of the preconditioner instead of the preconditioner itself, the study mitigates quantization errors in inverse fourth root computation at 4-bit precision. This strategic preservation of small singular values through eigenvector quantization proves pivotal. Moreover, the introduction of orthogonal rectification and linear square quantization mapping techniques further bolsters performance. Across diverse image classification tasks employing various DNN architectures, 4-bit Shampoo consistently matches the performance of its 32-bit counterpart while offering substantial memory savings. This pioneering work sets the stage for widespread adoption of memory-efficient second-order optimizers in large-scale DNN training.
Conclusion:
The introduction of the 4-bit second-order Shampoo optimizer marks a significant advancement in memory-efficient deep learning training. By maintaining performance while significantly reducing memory consumption, this innovation is poised to reshape the landscape of DNN optimization, making large-scale model training more accessible and efficient for various industries and applications.