- Challenges in accurately modeling magnetic hysteresis for optimizing performance of devices like electric machines and actuators.
- Limitations of traditional neural networks (RNNs, LSTM, GRUs) in generalizing to novel magnetic fields.
- Introduction of neural operators (DeepONet, FNO) to directly approximate the operator mapping H to B fields.
- Use of Preisach-based model dataset (FORCs, minor loops) normalized with min-max scaling.
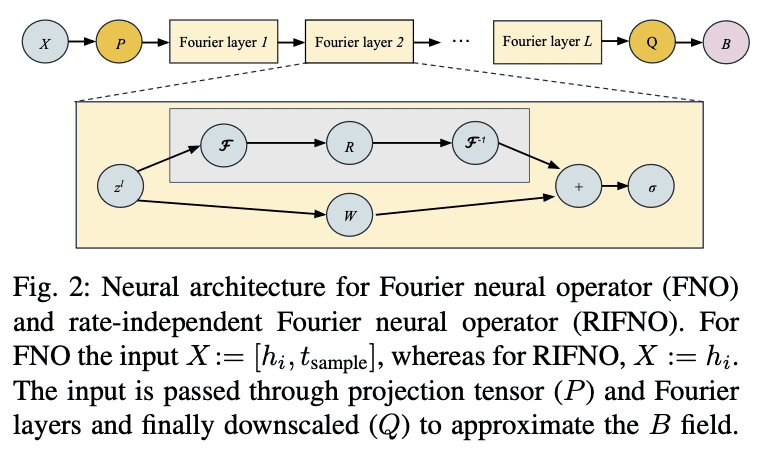
- DeepONet employs dual feedforward nets; FNO uses CNN with Fourier layers, enhancing accuracy.
- RIFNO variant excludes sampling array, suitable for rate-independent hysteresis modeling.
- Evaluation metrics (L2 norm relative error, MAE, RMSE) show superior performance of neural operators over traditional methods.
Main AI News:
The proposed approach tackles the challenge of modeling magnetic hysteresis with neural operators like Deep Operator Network (DeepONet) and Fourier Neural Operator (FNO), which offer enhanced accuracy and generalizability compared to traditional methods. Traditional neural networks such as RNNs, LSTM, and GRUs, while effective within specific training contexts, often fail to generalize to new magnetic fields due to their limitations in continuous function mapping. Neural operators overcome this by directly approximating the operator that maps applied magnetic fields (H) to magnetic flux density (B), enabling robust predictions under varying conditions.
This method leverages datasets from a Preisach-based model of material NO27-1450H, including first-order reversal curves (FORCs) and minor loops, normalized via min-max scaling. DeepONet employs a dual feedforward neural network architecture (branch and trunk nets) to approximate B fields, while FNO utilizes convolutional neural networks with Fourier layers to transform tensors and approximate B fields effectively. Introducing the rate-independent Fourier Neural Operator (RIFNO) further enhances adaptability by excluding the sampling array, ensuring accurate predictions across different sampling rates and scenarios of rate-independent hysteresis.
Evaluation metrics such as relative error in L2 norm, mean absolute error (MAE), and root mean squared error (RMSE) demonstrate the superior performance of neural operators. FNO exhibits minimal errors (relative error: 1.34e-3, MAE: 7.48e-4, RMSE: 9.74e-4), highlighting its efficacy in modeling magnetic hysteresis. Similarly, RIFNO shows robustness with low prediction errors across varied testing rates, underscoring its capability to generalize effectively. In contrast, traditional recurrent models like RNN, LSTM, and GRU exhibit higher errors and struggle with predictions for new magnetic fields, emphasizing the transformative potential of neural operators in this domain.
Conclusion:
The introduction of neural operators marks a significant advancement in modeling magnetic hysteresis, addressing critical limitations of traditional neural networks. By directly approximating the underlying operator mapping magnetic fields, these technologies offer enhanced accuracy and robustness in predicting hysteresis behavior under diverse conditions. This innovation is poised to drive efficiencies in designing and optimizing magnetic devices such as electric machines and actuators, promising broader applicability and reliability in real-world applications.