- DotaMath addresses the challenges LLMs face with complex mathematical reasoning.
- Traditional methods struggle with problem decomposition and feedback.
- Innovations include thought decomposition, intermediate process display, and self-correction.
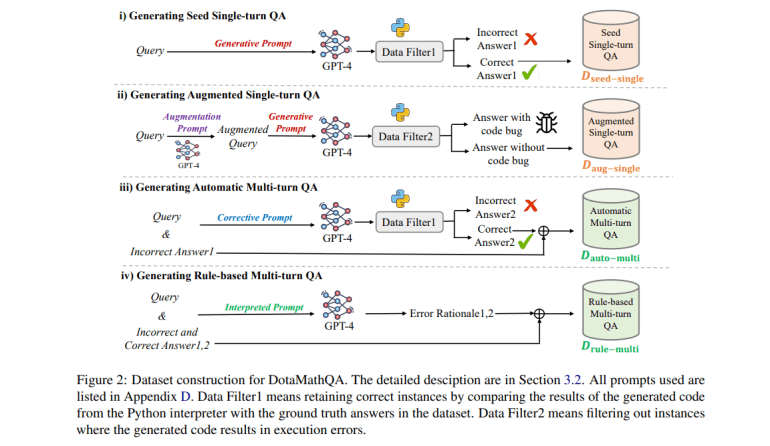
- DotaMathQA dataset, developed with GPT-4, supports task decomposition and code generation.
- The 7B model outperforms many larger models in elementary and complex tasks.
- DotaMath shows strong generalization on untrained datasets and incremental improvements.
Main AI News:
In the realm of large language models (LLMs), mathematical reasoning has long been a challenge, particularly when addressing complex tasks. Traditional approaches have struggled with decomposing intricate problems and providing adequate feedback through tools, leaving a gap in the LLMs’ ability to perform advanced mathematical analysis. Recent methodologies, while effective for simpler tasks, have not scaled well to more complex scenarios, underscoring the need for an advanced solution.
Recent advancements have seen improvements from Chain-of-Thought (COT) and Program-of-Thought (POT) methods, which introduced intermediate steps and coding tools to enhance problem-solving capabilities. Collaborative approaches blending COT with coding have shown notable accuracy gains. Researchers have also turned to data augmentation techniques, creating diverse mathematical datasets and synthetic question-answer pairs for Supervised Fine-Tuning (SFT). Despite these efforts, limitations persist, especially in managing complex tasks and providing thorough analysis.
To address these challenges, researchers from the University of Science and Technology of China and Alibaba Group have introduced DotaMath. This novel approach enhances LLMs’ mathematical reasoning through three key innovations. First, it employs a thought decomposition strategy, breaking down complex problems into manageable subtasks that leverage code assistance. Second, it features an intermediate process display, enabling detailed feedback from code interpreters to enhance analysis and response readability. Third, DotaMath integrates a self-correction mechanism, allowing the model to revise and improve its solutions upon initial failures. These advancements collectively aim to address the shortcomings of previous methods and significantly enhance LLMs’ capabilities in handling complex mathematical tasks.
DotaMath’s innovations include thought decomposition, intermediate process feedback, and self-correction. By breaking problems into subtasks, using code for solutions, and incorporating detailed feedback, DotaMath leverages the DotaMathQA dataset—developed with GPT-4’s help—to improve task decomposition, code generation, and error correction. This dataset includes single-turn and multi-turn QA data from existing and augmented queries, enabling fine-tuning of base models on reasoning trajectories. The result is a model that handles complex mathematical tasks more effectively than prior methods, overcoming limitations in LLMs’ mathematical reasoning.
DotaMath’s performance across mathematical reasoning benchmarks is impressive. Its 7B model excels beyond most 70B open-source models in elementary tasks such as GSM8K. In more complex scenarios like MATH, it outperforms both open-source and proprietary models, demonstrating the efficacy of its tool-based approach. The model’s strong generalization on untrained out-of-domain datasets and incremental improvements across different variations further highlight its advanced capabilities. Overall, DotaMath’s comprehensive approach—encompassing task decomposition, code assistance, and self-correction—proves highly effective in advancing LLMs’ mathematical reasoning.
Conclusion:
DotaMath’s advanced approach marks a significant leap in enhancing LLMs’ mathematical reasoning capabilities. By integrating decomposition strategies, detailed feedback mechanisms, and self-correction, DotaMath effectively overcomes the limitations of existing methods. This innovation not only addresses the persistent challenges in complex problem-solving but also sets a new benchmark for LLM performance in mathematical tasks. For the market, this advancement represents a critical development, suggesting that future LLMs could achieve higher accuracy and efficiency in diverse applications. The success of DotaMath underscores the potential for similar approaches to drive further breakthroughs in artificial intelligence, making it a notable example of progress in the field.