- Tensor conflicts crucial in various research areas, demanding optimal conflict sequences.
- Novel method refines standard greedy algorithm with an enhanced cost metric for improved efficiency.
- Previous methodologies include simulated annealing, genetic algorithms, and graph decomposition.
- Refined algorithm surpasses state-of-the-art implementations, offering broader problem coverage.
- Computation unfolds in three phases: Hadamard product, sequential contraction, and outer product.
- Refined algorithm incorporates diverse cost metrics as parameters for better adaptability.
- Two experiments conducted, focusing on solution quality and time-limited computation.
- Findings demonstrate a balance between expediency and efficacy for practical scenarios.
Main AI News:
Tensor conflicts present a pivotal avenue for resolving issues across various research domains, spanning from model enumeration to quantum circuitry, graph theory, and machine intelligence. However, to streamline computational expenses, determining an optimal conflict sequence remains paramount. While the outcome of computing the matrix product sequence A×B×CA×B×C remains constant, the associated computational expenses vary contingent on matrix dimensions. Furthermore, the cost of contracting tensors within networks escalates with the proliferation of tensor quantities. The trajectory employed to identify tensors ripe for contraction significantly impacts computational efficiency.
Historically, endeavors have been directed towards delineating efficient Contraction Paths (CPs) for tensor hypernetworks. Prevailing methodologies encompass simulated annealing and genetic algorithms, exhibiting superior efficacy for modest networks compared to standard greedy approaches. Alternatively, graph decomposition, leveraging Line-Graph (LG) and Factor-Tree (FT) methodologies, offers another avenue. LG employs structured graph analysis to discern contraction sequences, while FT facilitates preprocessing to handle high-rank tensors. A third avenue merges reinforcement learning (RL) with Graph Neural Networks (GNNs), catering to real and synthetic quantum circuits.
A pioneering team has unveiled a novel technique for refining tensor contraction paths by refining the standard greedy algorithm with an enhanced cost metric. The conventional greedy algorithm (SGA) predicates pairwise contractions for each step, anchored in a rudimentary cost function contingent on input and output tensor sizes. In contrast, the proposed approach augments this by appraising additional facets, employing diverse cost metrics to accommodate a broader problem spectrum. This methodology surpasses state-of-the-art implementations like Optimized Einsum (opt_einsum), occasionally eclipsing methodologies such as hypergraph partitioning amalgamated with greedy techniques.
Researchers harnessed SGA within opt_einsum to efficiently compute CPs for substantial tensor quantities. The CP computation unfolds across three phases:
- Hadamard product computation, entailing elementwise tensor multiplication.
- Sequential tensor contraction until all indices are exhausted, with each step selecting the lowest cost pair.
- Outer product computation, selecting pairs to minimize input size summation at each step.
Moreover, the refined greedy algorithm incorporates cost metrics as parameters, diverging from SGA’s singular cost function. During runtime, distinct cost functions are deployed, with the most fitting one selected to generate subsequent CPs.
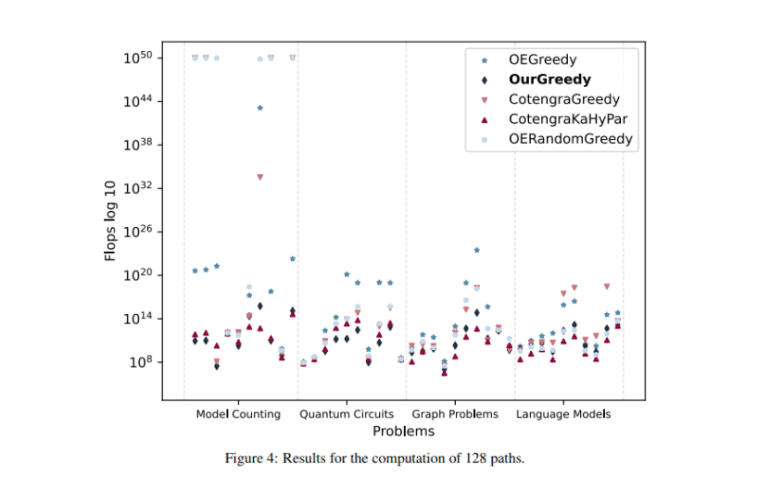
To gauge efficacy, CPs for ten scenarios are computed utilizing a multi-cost-function approach, juxtaposed against various algorithms, with flops serving as a yardstick. Two experiments were conducted: firstly, 128 paths computed per algorithm per scenario, focusing on solution quality sans time constraints; secondly, time-limited computation of 1 second, prioritizing a balance between expediency and efficacy for practical scenarios.
Conclusion:
The refinement of tensor contraction paths through an enhanced greedy algorithm signifies a leap forward in computational efficiency across diverse research domains. This innovation not only outperforms existing methodologies but also showcases a strategic balance between solution quality and time constraints, poised to revolutionize practical applications in the market. Businesses leveraging such advancements stand to gain a competitive edge in accelerating problem-solving capabilities and driving innovation.