- RL faces challenges with large discrete action spaces, hindering quick decision-making.
- KAUST and Purdue Univ. introduced Stochastic Q-learning, StochDQN, and StochDDQN to mitigate inefficiencies.
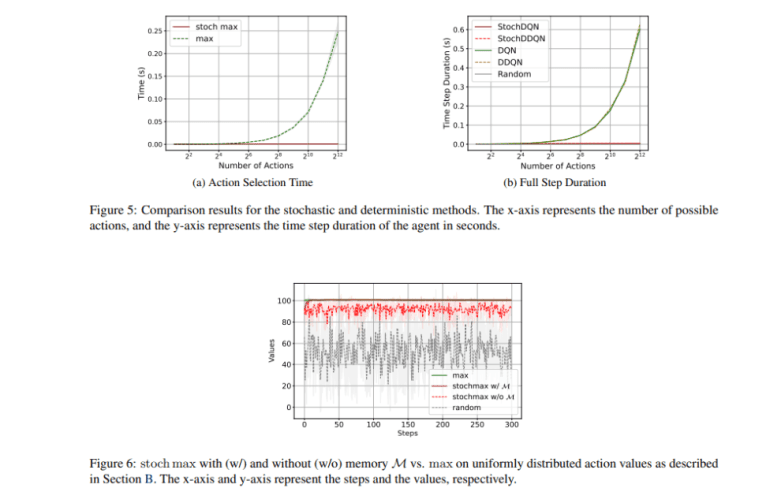
- These methods streamline computations by focusing on subsets of actions per iteration.
- Testing across various datasets showed faster convergence and higher efficiency compared to non-stochastic methods.
- Stochastic methods reduced computational time per step by 60-fold in tasks with 1000 actions.
Main AI News:
In the realm of machine learning, reinforcement learning (RL) stands as a pivotal domain where intelligent agents are groomed to navigate complex environments through interaction and feedback mechanisms. This feedback loop, comprised of actions and consequent rewards or penalties, forms the bedrock of RL algorithms. These algorithms have underpinned advancements in robotics, autonomous systems, and strategic gaming technologies, offering solutions to multifaceted challenges across scientific and industrial domains.
Navigating environments with expansive discrete action spaces presents a formidable obstacle in RL. Traditional methods such as Q-learning entail exhaustive evaluations of potential actions, rendering them impractical as action space complexity burgeons. This bottleneck inhibits real-world applications demanding swift and astute decision-making capabilities.
Enterprising minds from KAUST and Purdue University have devised pioneering stochastic value-based RL methodologies to tackle these bottlenecks head-on. Leveraging stochastic maximization techniques, their approaches – Stochastic Q-learning, StochDQN, and StochDDQN – streamline computational burdens by focusing on subsets of actions per iteration. This paradigm shift heralds scalable solutions adept at handling large action spaces with finesse.
Integrating stochastic maximization into RL frameworks, the research team implemented a suite of stochastic methods, including Stochastic Q-learning, StochDQN, and StochDDQN. Rigorous testing across diverse datasets, from Gymnasium environments like FrozenLake-v1 to MuJoCo control tasks such as InvertedPendulum-v4 and HalfCheetah-v4, showcased superior convergence and efficiency. By replacing traditional operations with stochastic counterparts, computational complexity dwindled, leading to faster convergence rates and enhanced efficiency.
Quantitative analyses underscored the efficacy of stochastic methodologies. In FrozenLake-v1, Stochastic Q-learning outperformed traditional Q-learning, achieving optimal cumulative rewards in half the steps. In InvertedPendulum-v4, StochDQN showcased a remarkable average return of 90 in 10,000 steps, eclipsing DQN’s performance which required 30,000 steps. Similarly, StochDDQN completed 100,000 steps in just 2 hours for HalfCheetah-v4, a task that demanded 17 hours for DDQN. Notably, the time per step plummeted from 0.18 seconds to 0.003 seconds in tasks with 1000 actions, marking a 60-fold surge in speed.
Conclusion:
The introduction of efficient stochastic methods by KAUST and Purdue University signifies a transformative shift in the RL landscape. These innovations promise enhanced efficiency and faster decision-making capabilities, which could revolutionize industries reliant on RL technologies. Companies should monitor and integrate these advancements to gain a competitive edge in dynamic markets.