TL;DR:
- LeanDojo is an open-source toolkit for LLM-based theorem proving, designed to overcome challenges faced by Large Language Models.
- It leverages the Lean proof assistant and provides resources, toolkits, and benchmarks for extracting data and interacting programmatically with Lean.
- ReProver, an LLM-based prover augmented with retrieval techniques, has been developed using LeanDojo, enabling efficient premise selection from a math library.
- LeanDojo’s program analysis capacity and retrieval mechanism enhance the prover’s performance and effectiveness.
- A new benchmark dataset has been created, showcasing ReProver’s ability to generalize to theorems with novel premises.
- LeanDojo offers a cost-effective and accessible solution for LLM-based theorem proving, eliminating the need for extensive computational resources.
Main AI News:
Can LLMs Generate Mathematical Proofs that can be Rigorously Checked? Discover LeanDojo: An Open-Source AI Playground Empowering Large Language Models in Proving Formal Theorems within the Lean Proof Assistant
Artificial Intelligence (AI) and Machine Learning (ML) have emerged as the driving forces behind transformative innovations in today’s world. As AI continues to advance, it is revolutionizing the way humans interact with machines. A key aspect of AI is reasoning, which plays a vital role in emulating human intelligence. In the realm of Artificial Intelligence, various approaches have been explored to prove theorems, such as Automated Theorem Proving (ATP). ATP involves the automatic generation of proofs for theorems formulated in formal logic. However, the sheer magnitude of the search space makes ATP challenging to implement effectively.
In response to the challenges posed by ATP, Interactive Theorem Proving (ITP) has emerged as an alternative paradigm. ITP involves the collaboration between human experts and software tools known as proof assistants to construct proofs. This collaborative approach provides a more flexible and efficient method for theorem proving.
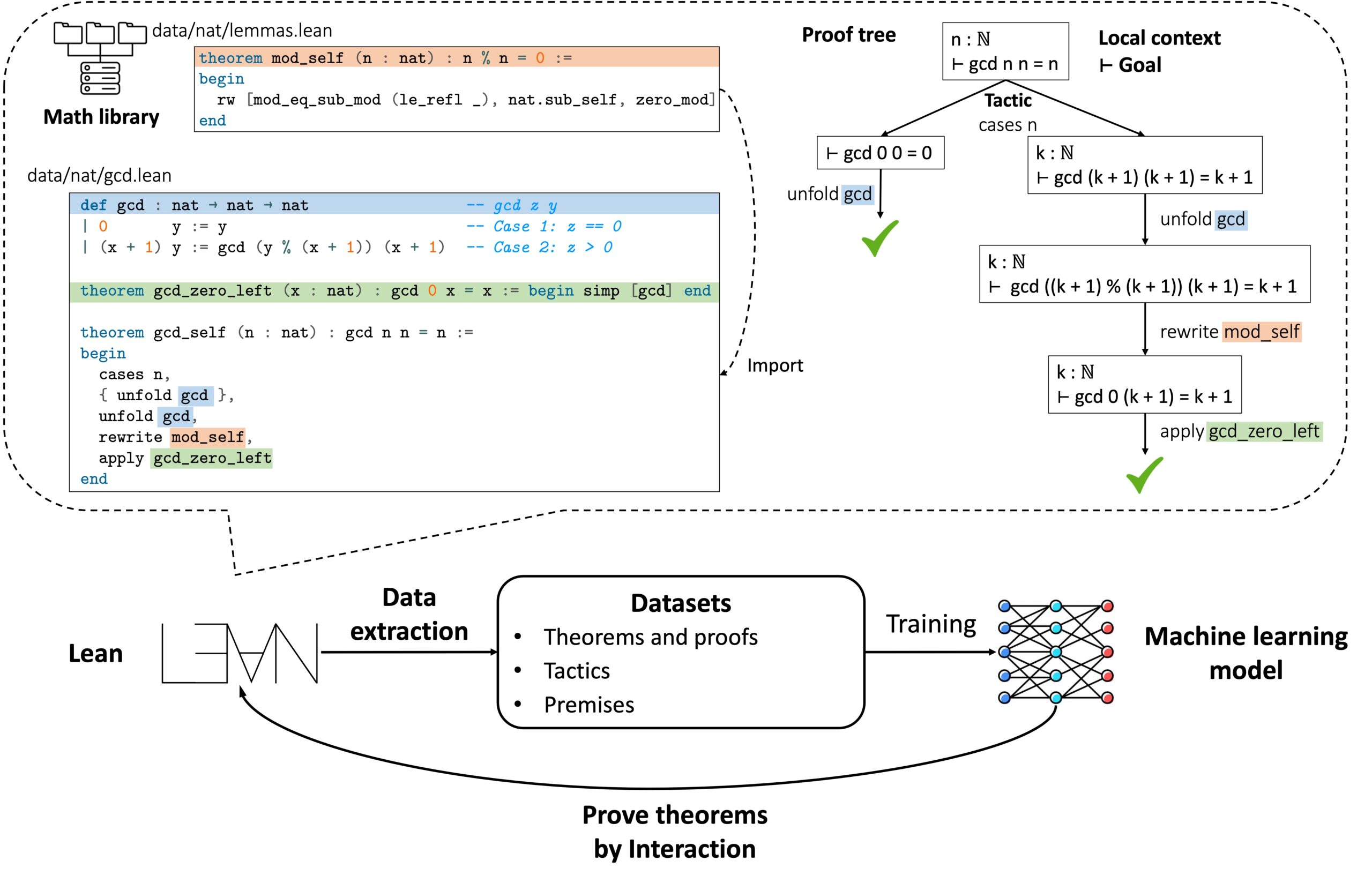
Despite their remarkable code generation capabilities, Large Language Models (LLMs) encounter obstacles when it comes to theorem proving. Issues like factuality and hallucination can hinder the accuracy and reliability of their proofs. To address these limitations, a collaborative team of researchers from prestigious institutions such as Caltech, NVIDIA, MIT, UC Santa Barbara, and UT Austin has developed LeanDojo. LeanDojo is an open-source toolkit specifically designed to facilitate LLM-based theorem proving. It revolves around the Lean proof assistant, a popular tool among mathematicians, offering a comprehensive set of resources for working with Lean and extracting valuable data.
LeanDojo incorporates data extraction, a process that involves gathering information from proof trees and intermediate proof states that may not be readily apparent in the original Lean code. This capability empowers models to interact programmatically with Lean, enabling them to observe proof states, execute proof actions or tactics, and receive feedback from Lean. The open-source Lean playground encompasses a range of elements, including toolkits, data, models, and benchmarks, providing a conducive environment for programmed interaction and data extraction within the proof domain.
One of the notable features of LeanDojo is its provision of fine-grained annotations for premises in proofs. This feature holds immense value for premise selection, a critical bottleneck in the theorem proving process. Leveraging LeanDojo’s data extraction capabilities, the researchers have developed ReProver, the first LLM-based prover augmented with retrieval techniques for selecting premises from an extensive mathematical library. Unlike previous methods that relied on private datasets, demanding substantial computational resources, ReProver is designed to be accessible and cost-effective. It operates efficiently with reduced computing power and can be trained using just one GPU per week.
By leveraging LeanDojo’s program analysis capacity, ReProver’s retrieval mechanism effectively identifies accessible premises and generates concrete examples of potential pitfalls. Consequently, ReProver demonstrates improved performance, while the retrieval procedure becomes more efficient. To facilitate evaluation and further research, the team has curated a new benchmark dataset comprising 96,962 theorems and proofs extracted from Lean’s comprehensive math library. This benchmark dataset incorporates a challenging data split, necessitating the prover to generalize to theorems that rely on novel premises not encountered during training. Experimental results have demonstrated that ReProver performs favorably when compared to non-retrieval baselines and even outperforms GPT-4 when trained and evaluated using this benchmark dataset.
Conclusion:
The introduction of LeanDojo and its capabilities in LLM-based theorem proving presents significant opportunities for the market. The open-source toolkit not only addresses the limitations of factuality and hallucination faced by Large Language Models, but it also provides a user-friendly environment for mathematicians and AI researchers to collaborate effectively. LeanDojo’s focus on accessibility, cost-effectiveness, and improved performance through premise selection and retrieval techniques positions it as a promising solution for businesses and organizations seeking to leverage AI-powered theorem proving capabilities. As the field of AI and theorem proving continues to evolve, LeanDojo’s contributions are likely to drive innovation and accelerate advancements in various sectors, including academia, research, and industry.